İçeriğe atlaNavigasyona atla

Month: April 2023

The Torsion Free Covers

by

Canan Özeren, Dokuz Eylül University. Date: 03rd of May, 2023, Wednesday, Time: 10:30 – 12:00. Place: Dokuz Eylül Univ., Tınaztepe Campus, Faculty of Science, Department of Mathematics, Room B206 (Online-Sakai-Graduate Meetings).

Abstract:  We talk about the existence and uniqueness (up to isomorphism) torsion-free covers of modules over an integral domain (see [1]). We show that the classical definition of torsion-free cover and the definition of an F-cover, where F is the class of the torsion-free modules, coincide.

References

[1] E. Enochs: Torsion-free covering modules. (1963)

+1 Step in Career: Student Clubs

by

The theme of our career event this month is +1 Step in Career: Student Clubs, and we host the Computer Science and Artificial Intelligence Club, Google Developer Students Clubs-DEU and Business Student Club in our event. The event is open to all mathematics department students and those who are interested. Those who are interested are asked to contact the moderator (Dr. Zübeyir Türkoğlu).

Speakers:

Date and Time: 17.04.2023, 11:30

Location: https://online.deu.edu.tr/
Channel: Kariyerde +1

On coGalois Groups III

by
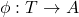
Canan Özeren, Dokuz Eylül University. Date: 12th of April, 2023, Wednesday, Time: 10:30 – 12:00. Place: Dokuz Eylül Univ., Tınaztepe Campus, Faculty of Science, Department of Mathematics, Room B206 (Online-Sakai-Graduate Meetings). Abstract:Torsion-free covers exist for abelian groups (see [1]). 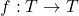The coGalois group of a torsion-free cover \phi: T \rightarrow A of an abelian group is defined in [2] as the group of f: T \rightarrow T s.t. 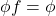\phi f= \phi and is denoted by 
*** QuickLaTeX cannot compile formula:
G(\phi)

*** Error message:
Cannot connect to QuickLaTeX server: cURL error 28: Operation timed out after 10001 milliseconds with 0 out of 0 bytes received
Please make sure your server/PHP settings allow HTTP requests to external resources ("allow_url_fopen", etc.)
These links might help in finding solution:
http://wordpress.org/extend/plugins/core-control/
http://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37
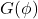
. The abelian groups for which the coGalois group is trivial were characterized in [3]. The notion of coGalois group can be defined in any category where we have a covering class. In [4], coGalois groups have been studied in the category of representations of the quiver q_2 : \cdot \rightarrow \cdot . We talk about the necessary and sufficient conditions for coGalois group, associated to a torsion free-cover of an object in (q_2, Z-mod) to be trivial. References [1] E. Enochs: Torsion-free covering modules. (1963) [2] E. Enochs, J. R. García Rozas and L. Oyonarte: Compact coGalois groups. (2000). [3] E. Enochs and J. Rada: Abelian groups which have trivial absolute coGalois group. (2005). [4] Paul Hill, Abelian group pairs having a trivial coGalois Group. (2006). [5] Molly Dukun, Phd Thesis [5] Molly Dukun, Phd Thesis

On rings whose cyclic modules have cyclic injective hulls

by

Prof. Dr. Christian Lomp, Department of Mathematics, University of Porto in Porto, Portugal. Date: 19th of April 2023, Wednesday. Time: 11:00. Place: Online/Microsoft Teams- Meeting ID: 351 128 968 15 Passcode: Gy4n4B

Abstract: In 1964, Barbara Osofsky proved in her PhD thesis that a ring whose cyclic modules are injective is semisimple Artinian. William Cadwell in his PhD thesis from 1966 studied when injective hulls of cyclic modules are cyclic and termed them hypercyclic rings. He characterised left perfect left hypercyclic rings as well as commutative local hypercyclic rings. In this talk we will revise the literature on rings whose cyclic modules have cyclic injective hulls and present some more recent results, obtained jointly with Mohamed Yousif and Yiqiang Zhou.