Ay: Nisan 2023

Burulmasız Örtüler

Yazarı:

Canan Özeren, Dokuz Eylül Üniversitesi.

Tarih: 03 Mayıs 2023, Çarşamba, Zaman: 10:30 – 12:00. Yer: Dokuz Eylül Üniv., Tınaztepe Yerleşkesi, Fen Fak. Matematik Böl. B206 nolu seminer/toplantı odası. (Online-Sakai-Graduate Meetings)

Özet: İntegral bölgesi üzerine modüller için burulmasız örtülerin her zaman var olması ve (isomorfiye göre) biricik olması hakkında konuşacağız (bkz. [1]). Klasik burulmasız örtü tanımının, F burulmasız modüller sınıfı olarak alındığında F-örtü tanımı ile uyumlu olduğunu göstereceğiz.

Kaynaklar

[1] E. Enochs: Torsion-free covering modules. (1963)

Kariyerde +1 Adım: Öğrenci Toplulukları

Yazarı:

Kariyer etkinliğimizin bu ayki teması Karityerde +1 Adım: Öğrenci toplulukları olup, etkinliğimizde Bilgisayar Bilimleri ve Yapay Zeka Topluluğu, Google Developer Students Clubs-DEU ve İşletme Öğrenci Topluluğu‘nu ağırlıyoruz. Etkinlik tüm matematik bölümü öğrencilerimize ve ilgilenenlere açıktır. İlgilenenlerin moderatör (Dr. Zübeyir Türkoğlu) ile iletişime geçmesi rica olunur.

Konuşmacılar:

Tarih ve Saat: 17.04.2023, 11:30

Yer: https://online.deu.edu.tr/
Kanal: Kariyerde +1

coGalois Gruplar Üzerine III

Yazarı:

Canan Özeren, Dokuz Eylül Üniversitesi.

Tarih: 12 Nisan, 2023, Çarşamba, Zaman: 10:30 – 12:00. Yer: Dokuz Eylül Üniv., Tınaztepe Yerleşkesi, Fen Fak. Matematik Böl. B206 nolu seminer/toplantı odası. (Online-Sakai-Graduate Meetings)

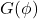Özet: Abel gruplar için burulmasız örtüler her zaman vardır (bkz. [1]). [2]’de, bir abel grubunun burulmasız örtüsü \phi:T \rightarrow A ‘nın coGalois grubu, \phi f = \phi şartını sağlayan f:T \rightarrow T grup homomorfizmalarını içeren bir grup olarak tanımlanmış ve G(\phi) ile gösterilmiştir. [3]’de, Abel grupları için coGalois gruplarının sadece birim morfizmayı içerdiği durumlar sınıflandırılmıştır. coGalois grup kavramı, örtü sınıfı olan herhangi bir kategoride de tanımlanabilir. [4]’de,  q_2 : \cdot \rightarrow \cdot kuiverinin temsil kategorisinde, coGalois grup kavramı çalışılmıştır. (q_2, Z-mod) kategorisinde bir nesne için burulmasız örtüden gelen coGalois grubun sadece birim morfizmayı içermesi için gerekli ve yeterli koşullar hakkında konuşacağız.

Kaynaklar

[1] E. Enochs: Torsion-free covering modules. (1963)

[2] E. Enochs, J. R. García Rozas and L. Oyonarte: Compact coGalois groups. (2000).

[3] E. Enochs and J. Rada: Abelian groups which have trivial absolute  coGalois group. (2005).

[4] Paul Hill, Abelian group pairs having a trivial coGalois Group. (2006). [5] Molly Dukun, Phd Thesis [5] Molly Dukun, Phd Thesis